数值计算实验

实验一

1.问题描述

求解线性方程组 Ax=b，其中 A 为 nⅹn 维的已知矩阵，b 为 n 维的已知向量，x 为 n 维的未知向量。

A 与 b 中的元素服从独立同分布的正态分布。令 n=10、50、100、200，测试计算时间并绘制曲线。

（1）高斯消去法。

（2）列主元消去法。

2.算法设计

高斯消去法

（1）消元：使用逐次消去未知数的方法把原线性方程组Ax = b化为与其等价的三角形线性方程组。

在这里使用将方程乘以某一乘数加到其它方程上以进行消元，乘数为两个未知数之商。得到等价的三角形线性方程组。

（2）回代：求解上三角线性方程组利用回代的方法，从下至上求出方程组中的一方程的未知数，然后逐层回代求出其它方程的未知数。

列主元消去法

与高斯消去法类似，在消元阶段进行交换行，选取绝对值最大的元素作为主元素，避免主元素为0，无法进行消元，以及当主元素很小时，作除数导致数值不稳定产生较大的误差。

回代方法和高斯消去法一致。

3.数值实验

随机构造出多个矩阵以及多个向量，矩阵和向量的维数n分别为10、50、100、200，同时使用高斯消去法，列主元消去法进行线性方程组的求解，比较两种算法的计算时间以及其计算时间与矩阵的维数（大小）的关系。

实验结果一：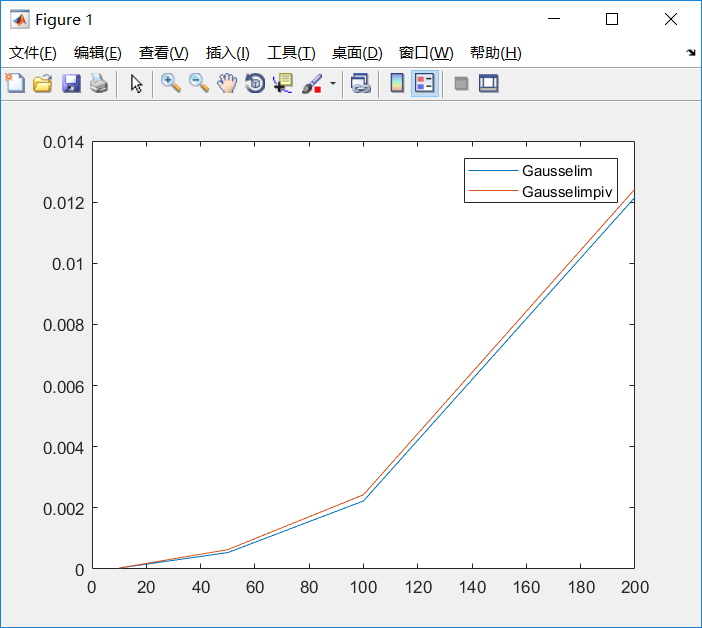

test1
test1

实验结果二：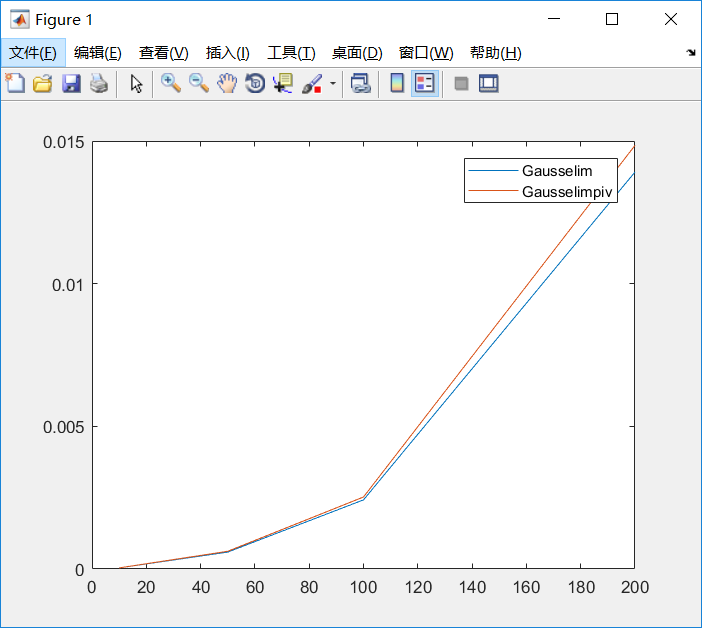

test1-1
test1-1

​

进行拟合：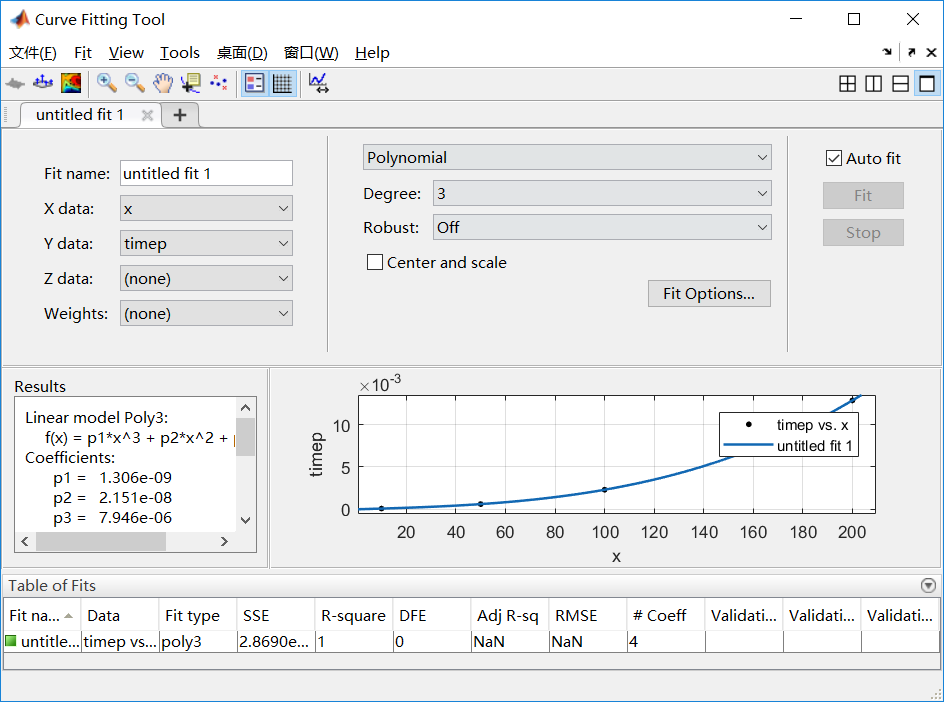

拟合
拟合

4.结果分析

通过进行计算时间的测试，并绘制曲线得到实验结果，观察可得列主元消去法因为要进行查找绝对值最大主元素，并进行交换使得计算时间比普通高斯消去方法稍长，但两者的计算时间还是相近。

另外当矩阵的维数（大小）变大，这种消元回代方法的计算时间也大幅度增长，通过函数的拟合发现其计算时间为O（n^3）的，n为矩阵的维数。

实验二

1.问题描述

求解线性方程组 Ax=b，其中 A 为 nⅹn 维的已知矩阵，b 为 n 维的已知向量，x 为 n 维的未知向量。

A 为对称正定矩阵，其特征值服从独立同分布的[0,1]间的均匀分布；b 中的元素服从独立同分布的正态分布。

令 n=10、50、100、200，分别绘制出算法的收敛曲线，横坐标为迭代步数，纵坐标为相对误差。比较Jacobi 迭代法、Gauss-Seidel 迭代法、逐次超松弛迭代法、共轭梯度法与高斯消去法、列主元消去法的计算时间。改变逐次超松弛迭代法的松弛因子，分析其对收敛速度的影响。

2.算法设计

Jacobi迭代法

雅可比迭代法的思想在于把当前的x初始量当成方程组的解，从而进行回代得出下一步x的近似解，这种方法每次迭代都使用上一次迭代的x，若迭代矩阵谱半径<1，则在一定迭代次数后，x会收敛成精确解。

Gauss-Seidel 迭代法

高斯-赛德尔迭代与雅可比迭代类似，但是在每次迭代之中使用变量的最新信息计算x(k+1)，是雅可比迭代法的改进。

逐次超松弛迭代法

逐次超松弛迭代是高斯-赛德尔迭代的一种修正，当w 为1 时即为高斯-赛德尔迭代，即在每一步的迭代后，对上一步的\(x^(k)\)和迭代后的x‘进行加权运算 x(k+1)=(1−w)∗x(k)+w∗x(k)x(k+1) = (1-w)*x(k)+ w*x(k)，超松弛迭代w>1，一般为1<w<2，相当于做外插，加快收敛速度。

共轭梯度法

将解线性方程组转化成求解一个等价的二次函数\(f(x) = 1/2* x^T * A *x - b^T *x\)极小化的问题，从任意起始点出发沿A的共轭方向进行线性搜索得到二次函数的极小点。

3.数值实验

四种迭代法的收敛

n = 10的收敛曲线：（SOR收敛因子w 为1.1）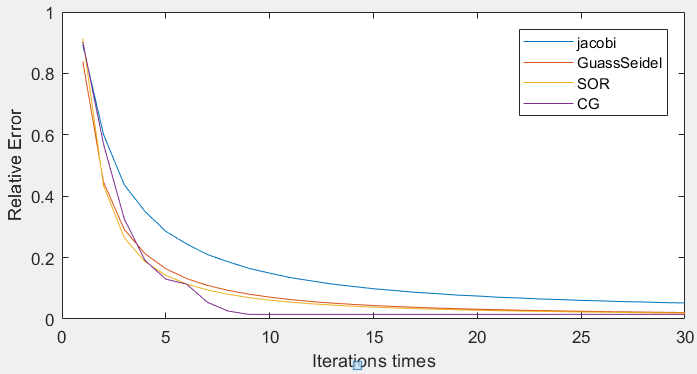

test2-1
test2-1

n = 50的收敛曲线：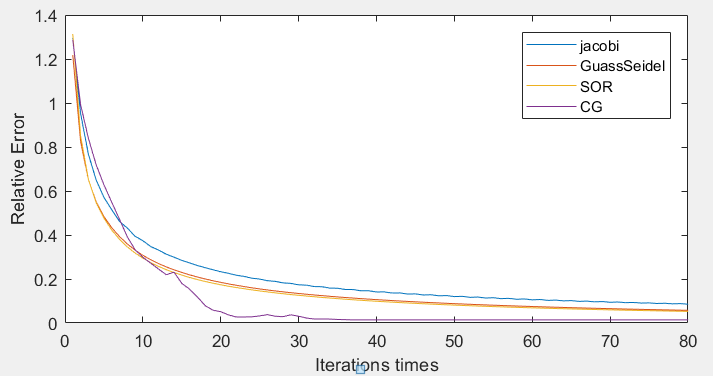

test2-2
test2-2

n = 100的收敛曲线：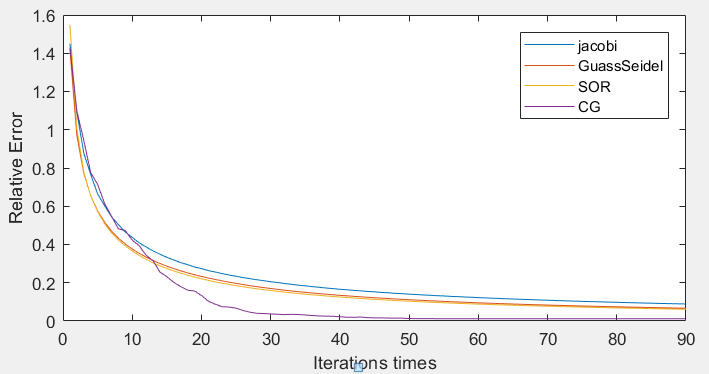

test2-3
test2-3

n = 200的收敛曲线：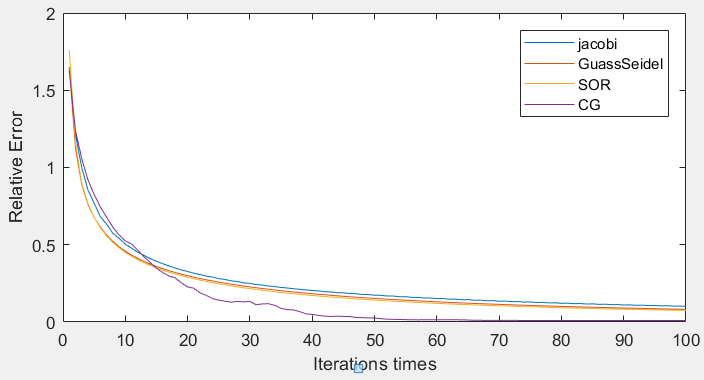

test2-4
test2-4

六种算法计算时间的比较

n = 10：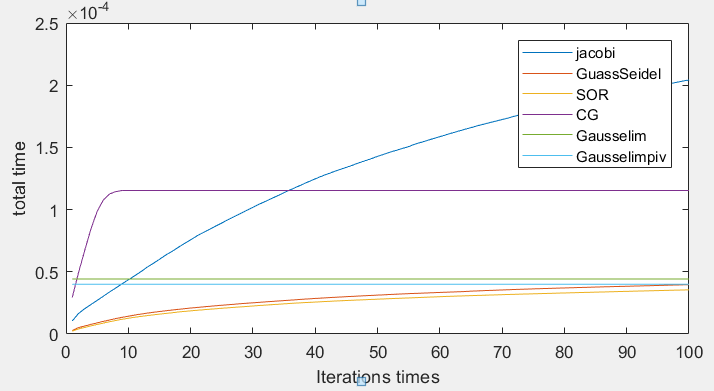

test2-5
test2-5

n = 50：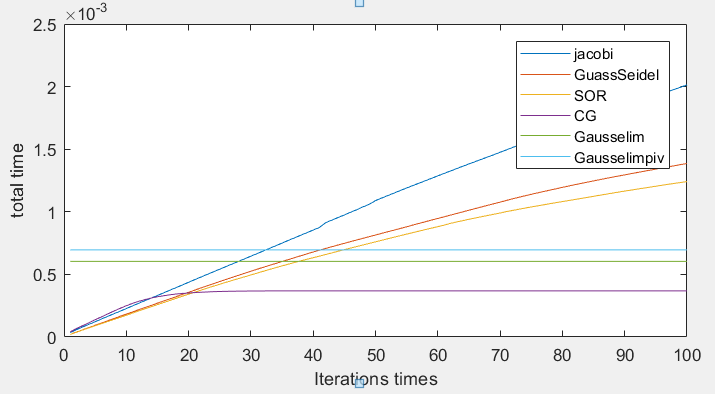

test2-6
test2-6

n = 100：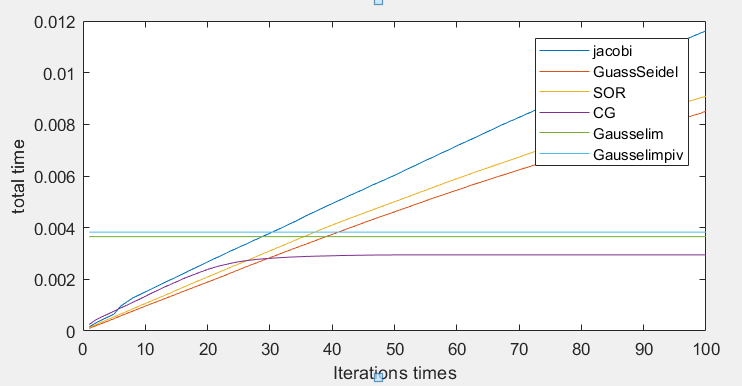

test2-7
test2-7

n = 200：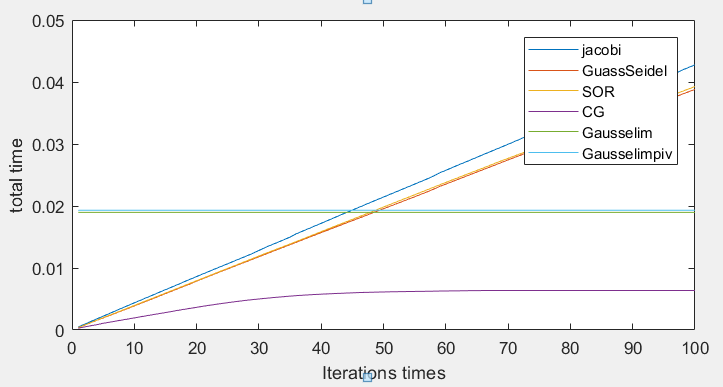

test2-8
test2-8

逐次超松弛迭代松弛因子（w）的影响

完整的图：（此时n =200）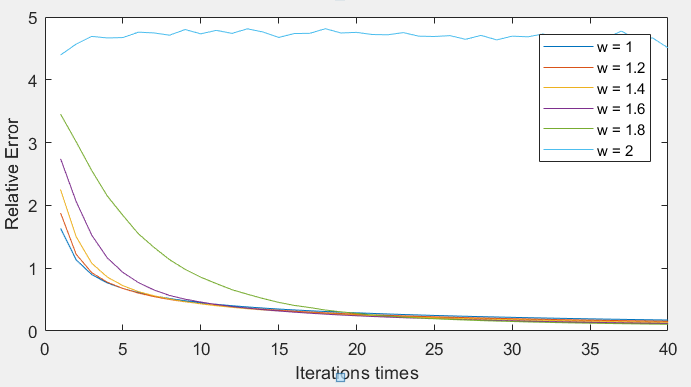

test3
test3

Y：（0，0.5）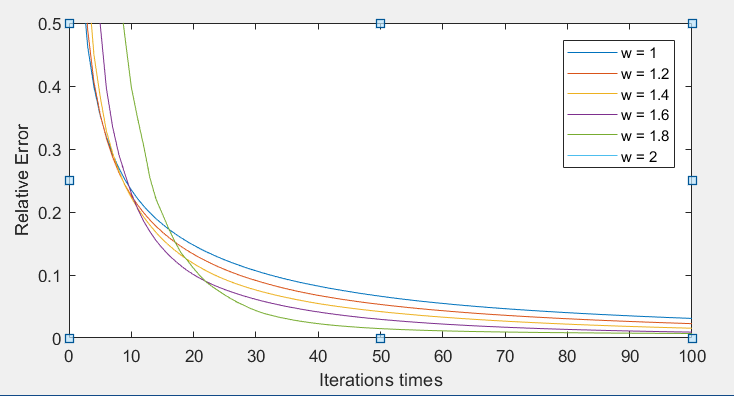

4.结果分析

  1. 根据实验二的结果可得在四种迭代法中，雅可比迭代法收敛性较差，据其改进的高斯-赛德尔则较好，而增加了加权平均进行外插运算的逐次超松弛迭代收敛速度更快，收敛速度最快的则是共轭梯度法。
  2. 而六种算法的计算时间中可以看出，当矩阵较小时，迭代法和消元法计算时间相差不大，矩阵较大时，共轭梯度法在计算时间中有着较大的优势，达到所需精度的迭代次数比其它迭代次数要少很多，并且每次迭代耗时较少。因为构造的矩阵并不是稀疏矩阵，所以在这种情况下，普通的消元法比其它迭代法所耗时间要少。
  3. 在分析松弛因子对收敛速度影响中，松弛因子对算法的收敛速度影响很大，选择合适的松弛因子能够减少算法的迭代次数，在较少的迭代次数得到较为精确的结果，对于不同的矩阵有着不同的最佳松弛因子，对于本次模拟的矩阵w较大则最好，但是w超过2之后，算法则不再收敛。

实验三

1.问题描述

在 Epinions 社交数据集中，每个网络节点可以选择信任其它节点。借鉴 Pagerank 的思想编写程序，对网络节点的受信任程度进行评分。在实验报告中，请给出伪代码。

2.算法设计

和pagerank相类似，预先给每个网络节点一个信任值Trust值为1/N，N为节点的数量，这样就能得到一个向量v代表每个节点的信任评分rank

v=[1/n,1/n,1/n,……]v = [1/n,1/n,1/n,……]

假定每个节点的对其他节点的总的信任程度为1，而且对每个其信任的节点都给予相同的信任程度，这样就可以得到一个信任转移矩阵A。

A（i，j）= 节点i对节点j的信任程度

每个节点的信任评分rank由信任它的节点决定，如果信任评分的节点本身的信任评分高，则给予的评分权重也高，反之给予评分权重较低。

所以通过计算

v‘ = Mv

即

v(i) = ∑其它节点信任评分v(j)*信任程度A(i,j)

可以得到新的一个信任评分，经过有限次的迭代，v’将会收敛稳定下来，得到的即是各个节点的信任评分。

改进

对于一些只信任自己的，对其它节点并未作出信任的网页节点，采用这种算法有2个缺点

1.使得信任评分都集中到那一循环的节点上。

2.对于新建立的网络节点来说，并不公平，因为一开始没有其他节点信任它，可能导致信任评分恶性循环。

因此添加一个权重占比α，原先的评分仅占α，然后默认每一个节点都对其它节点有一定程度（较小但不为0）的信任，这个信任程度影响评分所占的权重为1-α。因此迭代公式变为：

v(i)=∑v(j)∗A(i,j)∗α+(1−α)/Nv(i) = ∑v(j)*A(i,j)*α+(1-α)/N

α一般设定为0.85。

3.伪代码


A = [N,N];
α = 0.85;%设定权重

%构建转移矩阵，即信任关系矩阵
for i = 1: N
	for j = 1 : N
	A[i,j] = 1/n(n 为i的所有出链，即给予信任的节点数总数)
	end
end

%初始化信任评分rank
v0(1:N) = 1/N;
v = v0

%迭代
while norm(v-v0,'inf')>0.01 %当v逐渐收敛后结束迭代
	v0 = v;
	for i = 1: N
		sum = 0;
		for j = 1 : N
			%计算其它节点给予该节点的信任评分
			sum = sum + A(j,i)*v0(j)*α + (1-α)/N
		end
		v(i) = sum;
	end
end

disp(v');